“Just throw more VMs/resources at it“, This is what you will hear time and time again from cloud computing developers, but just how accurate is this statement?

In this post we put this statement to the test by running a number of experiments on the Google Cloud Platform. The task is straightforward, use Compute Engine VMs to covert a large volume of data from RDF to CSV format so it can be imported into Bigquery. The dataset is a structured extract from Wikipedia in 64 files totalling 50GB, the files were split between a number of n1-standard-2 instances by running 10 experiments, gradually ramping up VMs from 1 to 10.
Now, before I go into the results of the experiments let me introduce a few concepts. Usually in computing to speed up the processing of tasks these tasks get distributed between a number of computers so they can be processed in parallel. The hardness of this activity depends on the algorithm being used to process these tasks. Some algorithms are serial in nature and can’t be executed in parallel, on the other hand, other algorithms are embarrassingly (entirely) parallel and can be executed independently.
In parallel computing it’s possible to measure how fast a parallel algorithm runs compared to the correspondent serial algorithm, this fastness is called Speedup. A speedup of a parallel algorithms ![]() executed on
executed on ![]() VMs is calculated by dividing the runtime
VMs is calculated by dividing the runtime ![]() when using one VM by the runtime
when using one VM by the runtime ![]() when using
when using ![]() VMs as follow:
VMs as follow:
![Rendered by QuickLaTeX.com \[ s_n = \frac{t_1}{t_n} \]](https://omerio.com/wp-content/ql-cache/quicklatex.com-feb020892987678bca9400079703b8dc_l3.png)
The ideal or linear speedup is achieved when the number of VMs is proportional with the speed of the algorithm, this happens when the speedup is equal to the number of VMs i.e. ![]() . Another performance metric is Efficiency, which is a value between zero and one to indicate how well the VMs are utilised in executing the parallel algorithm, for example an efficiency of 0.5 (50%) or below isn’t good. Efficiency can be calculated as follows:
. Another performance metric is Efficiency, which is a value between zero and one to indicate how well the VMs are utilised in executing the parallel algorithm, for example an efficiency of 0.5 (50%) or below isn’t good. Efficiency can be calculated as follows:
![Rendered by QuickLaTeX.com \[ e_n = \frac{s_n}{n} = \frac{t_1}{t_n \times n} \]](https://omerio.com/wp-content/ql-cache/quicklatex.com-7142715751ec206679d55e26ea014403_l3.png)
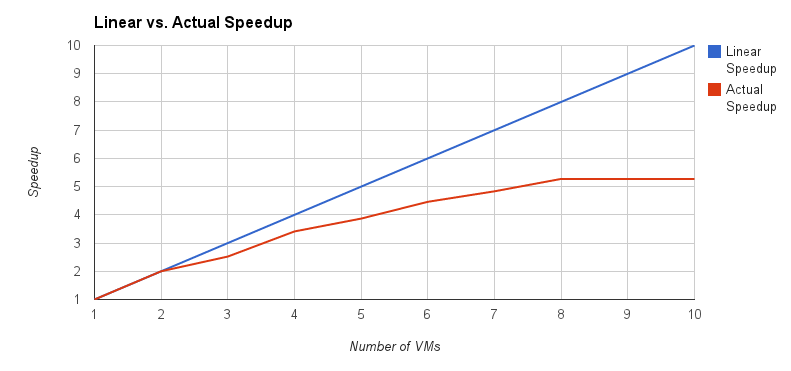
Now armed with these concepts, let’s see how well our parallel algorithm performed on the large Wikipedia dataset. The chart below shows the linear speedup in blue and the actual speedup in red, as seen from the chart linear speedup can only be achieved when using 2 VMs. Using more VMs results in a gradual decrease in the actual speedup compared to the linear speedup. When the number of VMs reaches 8 the speedup doesn’t increase any further, so adding more VMs beyond 8 is simply incurring additional cost, but is not getting the task done any quicker!.
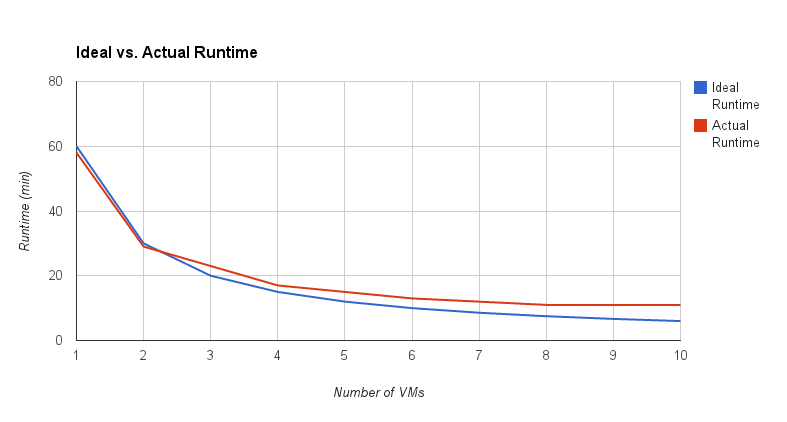
The chart below shows the correspondent runtime for both the ideal and actual speedup. For the ideal or linear speedup the runtime continue to reduce when more VMs are added, however the actual runtime hardly decreases beyond 6 VMs.
To summarise, from these experiments it’s evident that throwing more VMs at tasks doesn’t mean they will always get done quicker. This is mainly caused by the complexity and the nature of the tasks, so a better approach than ramping up VMs is to benchmark and optimise the algorithm so it performs better with more VMs.